This modified Caffe version supports layers with limited numerical precision. The layers in question use reduced word width for layer parameters and layer activations (inputs and outputs). As Ristretto follows the principles of Caffe, users already acquainted with Caffe will understand Ristretto quickly. The main additions of Ristretto are explained below.
Ristretto Layers
Ristretto introduces new layer types with limited numerical precision. These layers can be used through the traditional Caffe net description files (*.prototxt).
An example of a minifloat convolutional layer is given below:
layer {
name: "conv1"
type: "ConvolutionRistretto"
bottom: "data"
top: "conv1"
convolution_param {
num_output: 96
kernel_size: 7
stride: 2
weight_filler {
type: "xavier"
}
}
quantization_param {
precision: MINIFLOAT
mant_bits: 10
exp_bits: 5
}
}
This layer will use half precision (16-bit floating point) number representation. The convolution kernels, bias as well as layer activations are trimmed to this format.
Notice the three differences to a traditional convolutional layer:
typechanges toConvolutionRistretto- An additional layer parameter is added:
quantization_param - This layer parameter contains all the information used for quantization
Ristretto provides limited precision layers at src/caffe/ristretto/layers/.
Blobs
Ristretto allows for accurate simulation of resource-limited hardware accelerators. In order to stay with the Caffe principles, Ristretto reuses floating point blobs for layer parameters and outputs. This means that all numbers with limited precision are actually stored in floating point blobs.
Scoring
For scoring of quantized networks, Ristretto requires
- The 32-bit FP parameters of the trained network
- The network definition with reduced precision layers
The first item is the result of the traditional training in Caffe. Ristretto can test networks using full-precision parameters. The parameters are converted to limited precision on the fly, using round-nearest scheme by default.
As for the second item – the model description – you will either have to manually change the network description of your Caffe model, or use the Ristretto tool for automatic generation of a Google Protocol Buffer file.
# score the dynamic fixed point SqueezeNet model on the validation set* ./build/tools/caffe test --model=models/SqueezeNet/RistrettoDemo/quantized.prototxt \ --weights=models/SqueezeNet/RistrettoDemo/squeezenet_finetuned.caffemodel \ --gpu=0 --iterations=2000
*Before running this, please follow the SqueezeNet Example.
Fine-tuning
In order to improve a condensed network’s accuracy, it should always be fine-tuned. In Ristretto, the Caffe command line tool supports fine-tuning of condensed networks. The only difference to traditional training is that the network description file should contain Ristretto layers.
The following items are required for fine-tuning:
- The 32-bit FP network parameters
- Solver with hyper parameters for training
The network parameters are the result of full-precision training in Caffe.
The solver contains the path to the description file of the limited precision network. This network description is the same one that we used for scoring.
# fine-tune dynamic fixed point SqueezeNet* ./build/tools/caffe train \ --solver=models/SqueezeNet/RistrettoDemo/solver_finetune.prototxt \ --weights=models/SqueezeNet/squeezenet_v1.0.caffemodel
*Before running this, please follow the SqueezeNet Example.
Implementation details
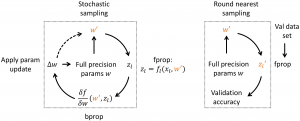
During this retraining procedure, the network learns how to classify images with limited word with parameters. Since the network weights can only have discrete values, the main challenge consists in the weight update. We adopt the idea of previous work (Courbariaux et al. [1]) which uses full precision shadow weights. Small weight updates are applied to the 32-bit FP weights w, whereas the discrete weights w‘ are sampled from the full precision weights. The sampling during fine-tuning is done with stochastic rounding, which was successfully used by Gupta et al. [2] to train networks in 16-bit fixed point.
[1] Matthieu Courbariaux, Yoshua Bengio, and Jean-Pierre David. Binaryconnect: Training deep neural networks with binary weights during propagations. In Advances in Neural Information Processing Systems, 2015.
[2] Suyog Gupta, Ankur Agrawal, Kailash Gopalakrishnan, and Pritish Narayanan. Deep learning with limited numerical precision. arXiv preprint, 2015.