This section covers 3 different strategies to quantize 32-bit floating point networks.
Dynamic Fixed Point
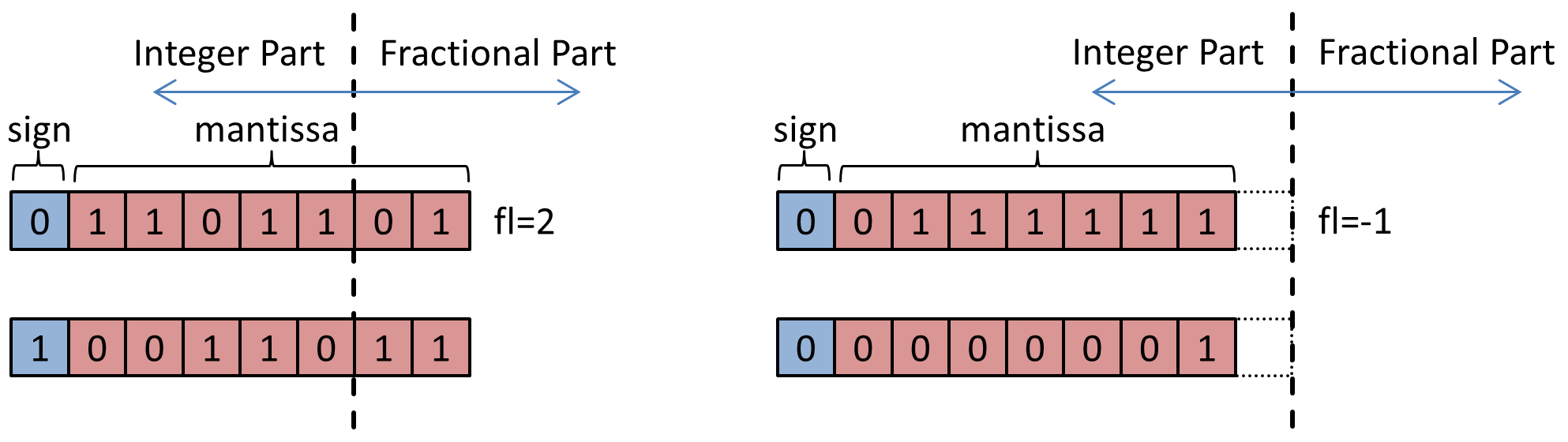
The different parts of a CNN have a significant dynamic range. In large layers, the outputs are the result of thousands of accumulations, thus the network parameters are much smaller than the layer outputs. Fixed point only has limited capability to cover a wide dynamic range. Dynamic fixed point as proposed by Courbariaux et al. [1] can be a good solution to overcome this problem. In dynamic fixed point, each number n is represented as follows: . Here B donates the bit-width, s the sign bit, fl is the fractional length, and x the mantissa bits. Since the intermediate values in a network have different ranges, it is desirable to group fixed point numbers into groups with constant fl. So the number of bits allocated to the fractional part is constant within that group, but different compared to other groups. Each network layer is split into three groups: one for the layer inputs, one for weights, and one for layer outputs. This allows to better cover the dynamic range of both layer activations and weights, as weights are normally significantly smaller.
The above picture shows an example of 4 dynamic fixed point numbers, which belong to two different groups. Notice the second group’s fractional length is negative. So the second group’s fractional length is -1, its integer length is 9, and its bit-width is 8.
[1] Matthieu Courbariaux, Yoshua Bengio, and Jean-Pierre David. Low precision arithmetic for deep learning. arXiv preprint, 2014.
Minifloat
Since the training of neural networks is done in floating point, it is an intuitive approach condense these models to bit-width reduced floating point numbers. In order to condense networks and reduce their computational and memory requirements, Ristretto can represent floating point numbers with much fewer bits than the IEEE-754 standard. We follow the standard to a large degree when going to 16bit, 8bit or even smaller numbers, but our format differs in some details. Namely, the exponent bias is lowered according to the number of bits assigned to the exponent: . Here exp_bits donates the number of bits assigned to the exponent. Another difference to the IEEE standard is that we don’t support denormalized numbers, INF and NaN. INF is replaced by saturated numbers, and denormalized numbers are replace by 0. Finally, the number of bits assigned to the exponent and mantissa part don’t follow a specific rule. To be more precise, Ristretto chooses the exponent bits such that no saturation occurs.
Multiplier-free arithmetic
With this approximation strategy, the multiplications are replaced by bit-shifts. Fully connected layers and convolutional layers consist of additions and multiplications, where multipliers require a much larger chip area. This motivated previous research to eliminate all multipliers by using integer-power-of-two weights [1]. These weights can be considered as minifloat numbers with zero mantissa bits. Multiplications between weights and layer activations turn into bit-shifts. Power-of-two parameters can be written as follows: . Here exp is an integer, typically negative for network parameters. Since small parameters close to zero don’t have much effect on the networks output, very small exponents can be ignored. Thus the possible exponent values can be significantly reduced. For AlexNet, we achieved good results with
. In this approximation mode, the activations are in dynamic fixed point format.
[1] Tang, Chuan Zhang, and Hon Keung Kwan. Multilayer feedforward neural
networks with single powers-of-two weights. IEEE Transactions on Signal Processing 41.8 (1993).